ANZIAM  J.  44 (2002), 169-180
Diffeomorphisms on $S^1$, projective structures and integrable systems

Partha Guha
  S.N. Bose National Centre for Basic Sciences
  JD Block, Sector-3
  Salt Lake
  Calcutta-700091
  India
  guha@BOSON.bose.res.in


Abstract
In this paper we consider a projective connection as defined by the nth-order Adler-Gelfand-Dikii (AGD) operator on the circle. It is well-known that the Korteweg-de Vries (KdV) equation is the archetypal example of a scalar Lax equation defined by a Lax pair of scalar nth-order differential (AGD) operators. 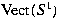In this paper we derive (formally) the KdV equation as an evolution equation of the AGD operator (at least for $n \leq 4$) under the action of $\operatorname{Vect}(S^1)$. The solutions of the AGD operator define an immersion ${\bf R} \to \mathbb{R}P^{n-1}$ in homogeneous coordinates. 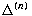In this paper we derive the Schwarzian KdV equation as an evolution of the solution curve associated with $\Delta^{(n)}$, for $n \leq 4$.
Download the article in PDF format (size 97 Kb)
TeXAdel Scientific Publishing ©  Australian MS