$n$-dimensional first integral and similarity solutions for two-phase flow

ANZIAM J. 44 (2003), 365-380

n-Dimensional first integral and similarity solutions for two-phase flow

S. W. Weeks
School of Mathematical Sciences
Queensland University of Technology
GPO Box 2434
Brisbane QLD 4001
Australia
s.weeks@fsc.qut.edu.au

G. C. Sander
Department of Civil and Building Engineering
Loughborough University
Loughborough
LE11 3TU
England
G.Sander@lboro.ac.uk

and

J.-Y. Parlange
Department of Biological and Environmental Engineering
Riley-Robb Hall
Cornell University
Ithaca NY
USA
jp58@cornell.edu

Abstract

This paper considers similarity solutions of the multi-dimensional transport equation for the unsteady flow of two viscous incompressible fluids. We show that in plane, cylindrical and spherical geometries, the flow equation can be reduced to a weakly-coupled system of two first-order nonlinear ordinary differential equations. This occurs when the two phase diffusivity $D(\theta)$ satisfies $(D/D')'=1/\alpha$ and the fractional flow function $f(\theta)$ satisfies $df/d\theta = \kappa D^{n/2}$ , where n is a geometry index (1, 2 or 3), $\alpha$ and $\kappa$ are constants and primes denote differentiation with respect to the water content $\theta$ . Solutions are obtained for time dependent flux boundary conditions. Unlike single-phase flow, for two-phase flow with n = 2 or 3, a saturated zone around the injection point will only occur provided the two conditions $\int_0^1D/(1-f) \, d\theta <\infty$ and $f'(1) \ne 0$ are satisfied. The latter condition is important due to the prevalence of functional forms of $f(\theta)$ in oil/water flow literature having the property

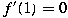Download the article in PDF format (size 170 Kb)

TeXAdel Scientific Publishing