ANZIAM J.
46 (2005), 317-330
|
The time fractional diffusion equation and the advection-dispersion equation
|
F. Huang
Department of Mathematics
Xiamen University
Xiamen 361005
China
fwliu@xmu.edu.cn
and
School of Mathematical Sciences
South China University of Technology
Guangzhou 510640
China
huangfh@scut.edu.cn
|
|
|
F. Liu
Department of Mathematics
Xiamen University
Xiamen 361005
China
and
School of Mathematical Sciences
Queensland University of Technology
Qld 4001
Australia
f.liu@qut.edu.au
|
|
|
Abstract
|
The time fractional diffusion equation with
appropriate initial and boundary conditions
in an
 -dimensional whole-space and half-space is
considered. Its solution has been obtained in
terms of Green functions by Schneider and Wyss.
For the problem in whole-space, an explicit
representation of the Green functions can
also be obtained. However, an explicit
representation of the Green functions for the
problem in half-space is difficult to
determine, except in the special cases -dimensional whole-space and half-space is
considered. Its solution has been obtained in
terms of Green functions by Schneider and Wyss.
For the problem in whole-space, an explicit
representation of the Green functions can
also be obtained. However, an explicit
representation of the Green functions for the
problem in half-space is difficult to
determine, except in the special cases
 with arbitrary with arbitrary
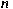 , or , or
 with arbitrary with arbitrary
 . In this paper, we solve these problems. By
investigating the explicit relationship
between the Green functions of the problem
with initial conditions in whole-space and that
of the same problem with initial and boundary
conditions in half-space, an explicit
expression for the Green functions corresponding
to the latter can be derived in terms of Fox
functions. We also extend some results of
Liu, Anh, Turner and Zhuang concerning the
advection-dispersion equation and obtain its
solution in half-space and in a bounded space
domain. . In this paper, we solve these problems. By
investigating the explicit relationship
between the Green functions of the problem
with initial conditions in whole-space and that
of the same problem with initial and boundary
conditions in half-space, an explicit
expression for the Green functions corresponding
to the latter can be derived in terms of Fox
functions. We also extend some results of
Liu, Anh, Turner and Zhuang concerning the
advection-dispersion equation and obtain its
solution in half-space and in a bounded space
domain.
|
Download the article in PDF format (size 113 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|