In this paper, we consider a coupled, nonlinear,
singular (in the sense that the reaction terms in
the equations are not Lipschitz continuous)
reaction-diffusion system, which arises from a
model of fractional order chemical autocatalysis
and decay, with positive initial data. In
particular, we consider the cases when the
initial data for the the dimensionless
concentration of the autocatalyst,
 , is of (a) , is of (a)
 or (b) or (b)
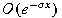 at large
at large  (dimensionless distance), where (dimensionless distance), where
 and and
 are constants. While initially the dimensionless
concentration of the reactant, are constants. While initially the dimensionless
concentration of the reactant,
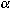 , is identically unity, we establish, by
developing the small- , is identically unity, we establish, by
developing the small-
 (dimensionless time) asymptotic structure of the
solution, that the support of (dimensionless time) asymptotic structure of the
solution, that the support of
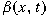 becomes finite in infinitesimal time in both
cases (a) and (b) above. The asymptotic form for
the location of the edge of the support of becomes finite in infinitesimal time in both
cases (a) and (b) above. The asymptotic form for
the location of the edge of the support of
 as as  is given in both cases. is given in both cases.
|