Bull. Austral. Math. Soc. 72(2) pp.283--290, 2005.

Characterisation of the isometric composition operators on the Bloch space

Flavia Colonna

Received: 3rd May, 2005

I wish to dedicate this article to Professor Maurice Heins for his ninetieth birthday.
I owe him a debt of gratitude for his great lectures which deeply stimulated my passion for complex analysis.
As a thesis advisor, he was always very patient and generous with his time.

Abstract

In this paper, we characterise the analytic functions $\varphi$ mapping the open unit disk $\Delta$ into itself whose induced composition operator C : f $\mapsto$ fo $\varphi$ is an isometry on the Bloch space. We show that such functions are either rotations of the identity function or have a factorisation $\varphi$ = gB where g is a non-vanishing analytic function from $\Delta$ into the closure of $\Delta$ , and B is an infinite Blaschke product whose zeros form a sequence {z_n } containing 0 and a subsequence {z_nj} satisfying the conditions $\bigl \vert$ g(z_nj) $\bigr \vert$ $\to$ 1, and

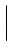$\displaystyle \lim _{{j\to \infty }}^{}$ $\displaystyle \prod _{{k\ne n_j}}^{}$ $\displaystyle \Bigl \vert$ $\displaystyle {\frac {{z_{n_{j}}-z_k}}{{1-\overline {z_{n_{j}}}z_k}}}$ $\displaystyle \Bigr \vert$ = 1.

Click to download PDF of this article (free access until July 2006)

or get the no-frills version

[an error occurred while processing this directive]

(Metadata: XML, RSS, BibTeX)

MathSciNet: MR2183409

Z'blatt-MATH: 02246390

References

J.M. Anderson, J. Clunie and Ch. Pommerenke;
On Bloch functions and normal functions,
J. Reine Angew. Math. 279 (1974), pp. 12--37. MR361090
L. Carleson;
An interpolation problem for bounded analytic functions,
Amer. J. Math. 80 (1958), pp. 921--930. MR117349
F. Colonna;
The Bloch constant of bounded analytic functions,
J. London Math. Soc. (2) 36 (1987), pp. 95--101. MR897677
F. Colonna;
Bloch and normal functions and their relation,
Rend. Circ. Mat. Palermo (2) 38 (1989), pp. 161--180. MR1029707
J.B. Garnett;
Bounded analytic functions (Acadademic Press, New York, 1981). MR628971
M.H. Heins;
A universal Blaschke product,
Arch. Math. 6 (1955), pp. 41--44. MR65644
C. Xiong;
Norm of composition operators on the Bloch space,
Bull. Austral. Math. Soc. 70 (2004), pp. 293--299. MR2094297

ISSN 0004-9727

Bulletin of the Australian Mathematical Society