A problem on rough parametric Marcinkiewicz functions

J. Austral. Math. Soc. 72 (2002), 13-21

Yong Ding
Department of Mathematics
Beijing Normal University
Beijing, 100875
P. R. China
dingy@bnu.edu.cn

Shanzhen Lu
Department of Mathematics
Beijing Normal University
Beijing, 100875
P. R. China
lusz@bnu.edu.cn

and

Kozo Yabuta
School of Science
Kwansei Gakuin University
Uegahara 1-1-155
Nishinomiya 662-8501
Japan
yabuta@kwansei.ac.jp

Abstract

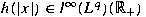In this note the authors give the $L^2(\mathbb{R}^n)$ boundedness of a class of parametric Marcinkiewicz integral $\mu^\rho_{\Omega,h}$ with kernel function $\Omega$ in $L\log^+ L(S^{n-1})$ and radial function $h(|x|)\in l^\infty(L^q)(\mathbb{R}_+)$ for $1<q\le\infty$ . As its corollary, the $L^p(\mathbb{R}^n)$ ( $2\le p<\infty$ ) boundedness of $\mu^{\ast,\rho}_{\Omega,h,\lambda}$ and $\mu^\rho_{\Omega,h,S}$ with $\Omega$ in $L\log^+ L(S^{n-1})$ and $h(|x|)\in l^\infty(L^q)(\mathbb{R}_+)$ are also obtained. Here $\mu^{\ast,\rho}_{\Omega,h,\lambda}$ and $\mu^\rho_{\Omega,h,S}$ are parametric Marcinkiewicz functions corresponding to the Littlewood-Paley $g^*_\lambda$ -function and the Lusin area function S, respectively.

Download the article in PDF format (size 81 Kb)

TeXAdel Scientific Publishing