J. Aust. Math. Soc.  74 (2003), 43-60

Parametrizing simple closed geodesy on

Thomas A. Schmidt   Oregon State University   Corvallis, OR 97331   USA   toms@math.orst.edu and Mark Sheingorn   CUNY - Baruch College   New York, NY 10010   USA   marksh@alum.dartmouth.org

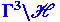
Abstract

We exhibit a canonical geometric pairing of the simple closed curves of the degree three cover of the modular surface, , with the proper single self-intersecting geodesics of Crisp and Moran. This leads to a pairing of fundamental domains for with Markoff triples. The routes of the simple closed geodesics are directly related to the above. We give two parametrizations of these. Combining with work of Cohn, we achieve a listing of all simple closed geodesics of length within any bounded interval. Our method is direct, avoiding the determination of geodesic lengths below the chosen lower bound.

Download the article in PDF format (size 164 Kb)

TeXAdel Scientific Publishing ©  Australian MS