J. Aust. Math. Soc.
74 (2003), 5-17
|
A characterization of weighted Bergman-Orlicz spaces on the unit ball in

|
Yasuo Matsugu
Department of Mathematical Sciences
Faculty of Science
Shinshu University
390-8621 Matsumoto
Japan
matsugu@math.shinshu-u.ac.jp
|
|
|
Jun Miyazawa
Department of Mathematical Sciences
Faculty of Science
Shinshu University
390-8621 Matsumoto
Japan
|
|
|
Abstract
|
Let
 denote the unit ball in denote the unit ball in
 , and , and
 the normalized Lebesgue measure on the normalized Lebesgue measure on
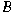 . For . For
 , define , define
 , ,
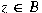 . Here . Here
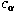 is a positive constant such
that is a positive constant such
that  . Let . Let
 denote the space of all holomorphic functions
in denote the space of all holomorphic functions
in  . For a twice differentiable, nondecreasing,
nonnegative strongly convex function . For a twice differentiable, nondecreasing,
nonnegative strongly convex function
 on the real line on the real line
 , define the Bergman-Orlicz space , define the Bergman-Orlicz space
 by by
|
![\[ A_{\varphi}(\nu_{\alpha})=\left\{f\in H(B):
\int_B \varphi(\log|f|)\, d\nu_{\alpha}<\infty\right\}.\]](img_files_abstracts/f120-img14.png)
|
In this paper we prove that a function
 is in is in
 if and only if if and only if
|
![\[\int_B \varphi''\big(\log|f(z)|\big)
\frac{|{\mathcal R} f(z)|^2}{|z|^2|f(z)|^2}
\big(1-|z|^2\big)^2\, d\nu_{\alpha}(z)<\infty,\]](img_files_abstracts/f120-img17.png)
|
where
 is the radial derivative of
is the radial derivative of
 . .
|
Download the article in PDF format (size 109 Kb)
|
|
|
|