J. Aust. Math. Soc.
74 (2003), 61-67
|
Manifolds that fail to be co-dimension 2 fibrators necessarily cover themselves
|
Young Ho Im
Department of Mathematics
Pusan National University
Pusan 609-735
Korea
yhim@pusan.ac.kr
|
|
|
Yongkuk Kim
Department of Mathematics
Kyungpook National University
Taegu 702-701
Korea
yongkuk@knu.ac.kr
|
|
|
Abstract
|
Let
 be a closed s-Hopfian be a closed s-Hopfian
 -manifold with residually finite, torsion free -manifold with residually finite, torsion free
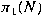 and finite and finite
 . Suppose that either . Suppose that either
 is finitely generated for all is finitely generated for all
 , or , or
 for for
 , or , or
 . We show that if . We show that if
 fails to be a co-dimension 2 fibrator, then fails to be a co-dimension 2 fibrator, then
 cyclically covers itself, up to homotopy type. cyclically covers itself, up to homotopy type.
|
Download the article in PDF format (size 67 Kb)
|
|
|
|