J. Aust. Math. Soc.
74 (2003), 421-436
|
On the asymptotic values of length functions in Krull and finitely generated commutative monoids
|
S. T. Chapman
Trinity University
Department of Mathematics
715 Stadium Drive
San Antonio, Texas 78212-7200
USA
schapman@trinity.edu
|
|
|
J. C. Rosales
Departamento de Álgebra
Universidad de Granada
E-18071 Granada
Spain
jrosales@ugr.es
|
|
|
Abstract
|
Let M
be a commutative cancellative atomic monoid. We
consider the behaviour of the asymptotic length
functions  and and  on M.
If M
is finitely generated and reduced, then we
present an algorithm for the computation of
both on M.
If M
is finitely generated and reduced, then we
present an algorithm for the computation of
both  and and  where where
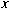 is a nonidentity element of M.
We also explore the values that the
functions is a nonidentity element of M.
We also explore the values that the
functions  and and  can attain when M
is a Krull monoid with torsion divisor class
group, and extend a well-known result of Zaks and
Skula by showing how these values can be used to
characterize when M is half-factorial. can attain when M
is a Krull monoid with torsion divisor class
group, and extend a well-known result of Zaks and
Skula by showing how these values can be used to
characterize when M is half-factorial.
|
Download the article in PDF format (size 144 Kb)
|
|
|
|