J. Aust. Math. Soc.  74 (2003), 351-378
Two results about $H^{\infty}$ functional calculus on analytic UMD Banach spaces

Christian Le Merdy
  Département de Mathématiques
  Université de Franche-Comté
  25030 Besancon Cedex
  France
  lemerdy@math.univ-fcomte.fr


Abstract
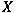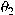Let $X$ be a Banach space with the analytic UMD property, and let $A$ and $B$ be two commuting sectorial operators on $X$ which admit bounded $H^{\infty}$ functional calculi with respect to angles $\theta_1$ and $\theta_2$ satisfying $\theta_1+ \theta_2<\pi$. It was proved by Kalton and Weis that in this case, $A+B$ is closed. The first result of this paper is that under the same conditions, $A+B$ actually admits a bounded $H^{\infty}$ functional calculus. Our second result is that given a Banach space $X$ and a number $1\leq p<\infty$, the derivation operator on the vector valued Hardy space $H^p(\mathbb{R};X)$ admits a bounded $H^{\infty}$ functional calculus if and only if $X$ has the analytic UMD property. This is an `analytic' version of the well-known characterization of UMD by the boundedness of the $H^{\infty}$ functional calculus of the derivation operator on vector valued $L^p$-spaces $L^p(\mathbb{R};X)$ for $1<p<\infty$ (Dore-Venni, Hieber-Prüss, Prüss).
Download the article in PDF format (size 243 Kb)
TeXAdel Scientific Publishing ©  Australian MS