J. Aust. Math. Soc.
75 (2003), 247-261
|
The
 - - mapping properties of convolution
operators with the affine arclength measure on space curves mapping properties of convolution
operators with the affine arclength measure on space curves
|
Youngwoo Choi
Department of Mathematics
Ajou University
Suwon 442-749
Korea
youngwoo@ajou.ac.kr
|
|
|
Abstract
|
The
 -improving properties of convolution operators
with measures supported on space curves have
been studied by various authors. If the
underlying curve is non-degenerate, the
convolution with the (Euclidean) arclength
measure is a bounded operator from -improving properties of convolution operators
with measures supported on space curves have
been studied by various authors. If the
underlying curve is non-degenerate, the
convolution with the (Euclidean) arclength
measure is a bounded operator from
 into into
 . Drury suggested that in case the underlying
curve has degeneracies the appropriate measure
to consider should be the affine arclength
measure and he obtained a similar result for
homogeneous curves . Drury suggested that in case the underlying
curve has degeneracies the appropriate measure
to consider should be the affine arclength
measure and he obtained a similar result for
homogeneous curves
 , ,
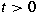 for for
 . This was further generalized by Pan to curves . This was further generalized by Pan to curves
 , ,
 for for
 , ,
 . In this article, we will extend Pan's result
to (smooth) compact curves of finite type whose
tangents never vanish. In addition, we give an
example of a flat curve with the same mapping
properties. . In this article, we will extend Pan's result
to (smooth) compact curves of finite type whose
tangents never vanish. In addition, we give an
example of a flat curve with the same mapping
properties.
|
Download the article in PDF format (size 113 Kb)
|
|
|
|