New proofs are given of the fundamental results
of Bader, Lunardon and Thas relating flocks of
the quadratic cone in PG(3, q),
q odd, and BLT-sets of Q(4, q).
We also show that there is a unique BLT-set
of H(3, 9).
The model of Penttila for Q(4, q),
q odd, is extended to Q(2m, q)
to construct partial flocks of size
qm/2 + m/2 - 1
of the cone 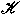 in PG(2m - 1, q)
with vertex a point and base Q(2m - 2, q), where
q is congruent to 1 or 3 modulo 8 and
m is even. These partial flocks are larger than
the largest previously known for
m > 2. Also, the example of O'Keefe and Thas of a
partial flock of in PG(2m - 1, q)
with vertex a point and base Q(2m - 2, q), where
q is congruent to 1 or 3 modulo 8 and
m is even. These partial flocks are larger than
the largest previously known for
m > 2. Also, the example of O'Keefe and Thas of a
partial flock of 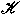 in PG(5, 3)
of size 6 is generalised to a partial flock of
the cone in PG(5, 3)
of size 6 is generalised to a partial flock of
the cone 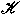 of PG(2pn - 1, p)
of size 2pn, for any prime p
congruent to 1 or 3 modulo 8, with the
corresponding partial BLT-set of Q(2pn, p)
admitting the symmetric group of degree 2pn + 1. of PG(2pn - 1, p)
of size 2pn, for any prime p
congruent to 1 or 3 modulo 8, with the
corresponding partial BLT-set of Q(2pn, p)
admitting the symmetric group of degree 2pn + 1.
|