J. Aust. Math. Soc.  77 (2004), 191-196
On the chromatic number of plane tilings

D. Coulson
  Department of Mathematics and Statistics
  The University of Melbourne
  VIC 3010
  Australia
  d.coulson@ms.unimelb.edu.au


Abstract
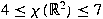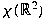It is known that $4\leq \chi (\mathbb{R}^2)\leq 7$, where $\chi (\mathbb{R}^2)$ is the number of colours necessary to colour each point of Euclidean 2-space so that no two points lying distance 1 apart have the same colour. Any lattice-sublattice colouring scheme for 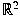$\mathbb{R}^2$ must use at least 7 colours to have an excluded distance. This article shows that at least 6 colours are necessary for an excluded distance when convex polygonal tiles (all with area greater than some positive constant) are used as the colouring base.
Download the article in PDF format (size 71 Kb)
TeXAdel Scientific Publishing ©  Australian MS