J. Aust. Math. Soc.
78 (2005), 109-147
|
Heat kernels on homogeneous spaces
|
C. M. P. A. Smulders
Department of Mathematics and Comp. Sci.
Eindhoven University of Technology
P.O. Box 513
5600 MB Eindhoven
The Netherlands
camsmul@cs.com
|
|
|
Abstract
|
Let
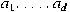 be a basis of the Lie algebra be a basis of the Lie algebra
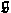 of a connected Lie group of a connected Lie group
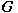 and let and let 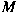 be a Lie subgroup of be a Lie subgroup of 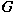 . If . If 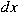 is a non-zero positive quasi-invariant regular
Borel measure on the homogeneous space is a non-zero positive quasi-invariant regular
Borel measure on the homogeneous space
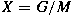 and and 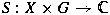 is a continuous cocycle, then under a rather
weak condition on is a continuous cocycle, then under a rather
weak condition on 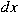 and and 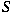 there exists in a natural way a (weakly*) continuous representation there exists in a natural way a (weakly*) continuous representation
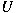 of of 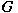 in in 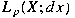 for all for all ![$p\in [1,\infty]$](img_files_abstracts/q102-img14.png) . Let . Let
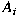 be the infinitesimal generator with respect to be the infinitesimal generator with respect to
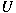 and the direction and the direction
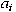 for all for all
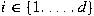 . We consider . We consider
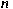 -th order strongly elliptic operators -th order strongly elliptic operators
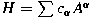 with complex coefficients with complex coefficients
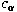 . We show that the semigroup . We show that the semigroup
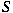 generated by the closure of generated by the closure of
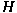 has a reduced heat kernel has a reduced heat kernel
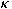 and we derive upper bounds for and we derive upper bounds for
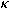 and all its derivatives. and all its derivatives.
|
Download the article in PDF format (size 336 Kb)
|
|
|
|