Let  be a finite-dimensional Lie algebra over the
field be a finite-dimensional Lie algebra over the
field  . The Ado-Iwasawa Theorem asserts the existence
of a finite-dimensional . The Ado-Iwasawa Theorem asserts the existence
of a finite-dimensional 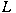 -module which gives a faithful representation -module which gives a faithful representation  of of 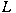 . Let . Let  be a subnormal subalgebra of be a subnormal subalgebra of  , let , let  be a saturated formation of soluble Lie algebras
and suppose that be a saturated formation of soluble Lie algebras
and suppose that  . I show that there exists a module . I show that there exists a module  with the extra property that it is with the extra property that it is  -hypercentral as -hypercentral as 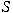 -module. Further, there exists a module -module. Further, there exists a module
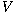 which has this extra property simultaneously for
every such which has this extra property simultaneously for
every such
 and and 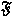 , along with the Hochschild extra that , along with the Hochschild extra that
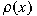 is nilpotent for every is nilpotent for every  with with  nilpotent. In particular,
if nilpotent. In particular,
if 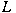 is supersoluble, then it has a faithful
representation by upper triangular matrices. is supersoluble, then it has a faithful
representation by upper triangular matrices.
|