J. Aust. Math. Soc.  80 (2006), 13-44
Partitions into large unequal parts from a general sequence

Kevin John Fergusson
  17 Blackdown way
  Karrinyup WA 6018
  Australia
  kevinjohnfergusson@hotmail.com


Abstract
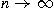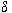An asymptotic estimate is obtained for the number of partitions of the positive integer n into unequal parts coming from a sequence u, with each part greater than m, under suitable conditions on the sequence u. The estimate holds uniformly with respect to integers m such that $0\le m \le n^{1-\delta }$, as $n\to\infty $, where $\delta $ is a given real number, such that $0<\delta < 1$.
Download the article in PDF format (size 234 Kb)
Australian Mathematical Publishing Association Inc. ©  Australian MS