J. Aust. Math. Soc.
80 (2006), 45-63
|
Seminormal and subnormal subgroup lattices for transitive permutation groups
|
Cheryl E. Praeger
School of Mathematics and Statistics
The University of Western Australia
35 Stirling Highway
Crawley WA 6009
Australia
praeger@maths.uwa.edu.au
|
|
|
Abstract
|
Various lattices of subgroups of a finite
transitive permutation group G
can be used to define a set of `basic'
permutation groups associated with
G
that are analogues of composition factors for
abstract finite groups. In particular,
G
can be embedded in an iterated wreath product of
a chain of its associated basic permutation
groups. The basic permutation groups
corresponding to the lattice
 of all subgroups of G
containing a given point stabiliser are a set of
primitive permutation groups. We introduce two
new subgroup lattices contained in of all subgroups of G
containing a given point stabiliser are a set of
primitive permutation groups. We introduce two
new subgroup lattices contained in
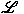 , called the seminormal subgroup lattice and the
subnormal subgroup lattice. For these lattices
the basic permutation groups are quasiprimitive
and innately transitive groups, respectively. , called the seminormal subgroup lattice and the
subnormal subgroup lattice. For these lattices
the basic permutation groups are quasiprimitive
and innately transitive groups, respectively.
|
Download the article in PDF format (size 151 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|