J. Aust. Math. Soc.
80 (2006), 263-272
|
On semiprime segments of rings
|
R. Mazurek
Faculty of Computer Science
Bialystok Technical University
Wiejska 45A
15-351 Bialystok
Poland
mazurek@pb.bialystok.pl
|
|
|
|
|
Abstract
|
A semiprime segment of a ring
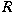 is a pair is a pair
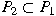 of semiprime ideals of of semiprime ideals of
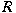 such that such that
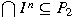 for all ideals for all ideals
 of of
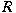 with with
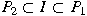 . In this paper semiprime segments with . In this paper semiprime segments with
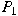 a comparizer ideal are classified as either
simple, exceptional, or archimedean, extending to
several classes of rings a classification known
for right chain rings. These three types of
semiprime segments are also characterized in
terms of the pseudo-radical. a comparizer ideal are classified as either
simple, exceptional, or archimedean, extending to
several classes of rings a classification known
for right chain rings. These three types of
semiprime segments are also characterized in
terms of the pseudo-radical.
|
Download the article in PDF format (size 88 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|