J. Aust. Math. Soc.
80 (2006), 359-366
|
Characterizing rings by a direct decomposition property of their modules
|
|
|
|
S. Tariq Rizvi
Department of Mathematics
The Ohio State University at Lima
Lima
Ohio 45804
USA
rizvi.1@osu.edu
|
|
|
Abstract
|
A module
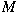 is said to satisfy the condition is said to satisfy the condition
 if if
 is a direct sum of a projective module and a
quasi-continuous module. In an earlier paper, we
described the structure of rings over which every
(countably generated) right module satisfies is a direct sum of a projective module and a
quasi-continuous module. In an earlier paper, we
described the structure of rings over which every
(countably generated) right module satisfies
 , and it was shown that such a ring is right
artinian. In this note some additional properties
of these rings are obtained. Among other results,
we show that a ring over which all right modules
satisfy , and it was shown that such a ring is right
artinian. In this note some additional properties
of these rings are obtained. Among other results,
we show that a ring over which all right modules
satisfy  is also left artinian, but the property is also left artinian, but the property
 is not left-right symmetric. is not left-right symmetric.
|
Download the article in PDF format (size 72 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|