Omitted rays and wedges of fractional Cauchy transforms

J. Aust. Math. Soc. 80 (2006), 367-373

Omitted rays and wedges of fractional Cauchy transforms

R. A. Hibschweiler
University of New Hampshire
Department of Mathematics and Statistics
Durham, NH 03824
USA
rah2@cisunix.unh.edu

and

T. H. Macgregor
Bowdoin College
Department of Mathematics
Brunswick, ME 04011
USA

Abstract

For $\alpha>0$ let $\mathcal{F}_{\alpha}$ denote the set of functions which can be expressed

$f(z)= \int_{|\zeta|=1} \frac1{(1-\overline{\zeta}z)^{\alpha}}\, d\mu(\zeta) \quad\text{for }\ |z|<1,$

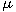where $\mu$ is a complex-valued Borel measure on the unit circle. We show that if

is an analytic function in $\Delta=\{z\in\mathbb{C}: |z|<1\}$ and there are two nonparallel rays in $\mathbb{C}\backslash f(\Delta)$ which do not meet, then $f\in \mathcal{F}_{\alpha}$ where $\alpha\pi$ denotes the largest of the two angles determined by the rays. Also if the range of a function analytic in $\Delta$ is contained in an angular wedge of opening $\alpha\pi$ and $1<\alpha<2$ , then $f\in \mathcal{F}_{\alpha}$ .

Download the article in PDF format (size 64 Kb)

Australian Mathematical Publishing Association Inc.