The double cover relative to a convex domain and the relative isoperimetric inequality

J. Aust. Math. Soc. 80 (2006), 375-382

The double cover relative to a convex domain and the relative isoperimetric inequality

Jaigyoung Choe
Department of Mathematics
Seoul National University
Seoul 151-742
Korea
choe@math.snu.ac.kr

Abstract

We prove that a domain $\Omega$ in the exterior of a convex domain

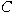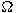in a four-dimensional simply connected Riemannian manifold of nonpositive sectional curvature satisfies the relative isoperimetric inequality $64\pi^2 \operatorname{Vol}(\Omega)^3 \leq \operatorname{Vol}(\partial \Omega \sim \partial C)^4$ . Equality holds if and only if $\Omega$ is an Euclidean half ball and $\partial \Omega \sim \partial C$ is a hemisphere.

Download the article in PDF format (size 66 Kb)

Australian Mathematical Publishing Association Inc.