J. Aust. Math. Soc.
80 (2006), 297-315
|
Operator algebras with a reduction property
|
James A. Gifford
Mathematical Sciences Institute
Australian National University
Canberra, ACT 0200
Australia
giffordj@maths.anu.edu.au
|
|
|
Abstract
|
Given a representation
 of a Banach algebra of a Banach algebra
 on a Hilbert space on a Hilbert space
 , ,
 is said to have the reduction property as an is said to have the reduction property as an
 -module if every closed invariant subspace of -module if every closed invariant subspace of
 is complemented by a closed invariant subspace; is complemented by a closed invariant subspace;
 has the total reduction property if for every
representation has the total reduction property if for every
representation  , ,
 has the reduction property. We show that a has the reduction property. We show that a
 -algebra has the total reduction property if and
only if all its representations are similar to -algebra has the total reduction property if and
only if all its representations are similar to
 -representations. The question of whether all -representations. The question of whether all
 -algebras have this property is the famous
`similarity problem' of Kadison. We conjecture
that non-self-adjoint operator algebras with the
total reduction property are always isomorphic to -algebras have this property is the famous
`similarity problem' of Kadison. We conjecture
that non-self-adjoint operator algebras with the
total reduction property are always isomorphic to
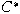 -algebras, and prove this result for operator
algebras consisting of compact operators. -algebras, and prove this result for operator
algebras consisting of compact operators.
|
Download the article in PDF format (size 145 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|