J. Aust. Math. Soc.
81 (2006), 35-47
|
The structure of groups whose subgroups are permutable-by-finite
|
M. De Falco
Dipartimento di Matematica e Applicazioni
Università di Napoli Federico II
Complesso Universitario Monte S. Angelo
Via Cintia
I–80126 Napoli
Italy
mdefalco@unina.it
|
|
F. de Giovanni
Dipartimento di Matematica e Applicazioni
Università di Napoli Federico II
Complesso Universitario Monte S. Angelo
Via Cintia
I–80126 Napoli
Italy
degiovan@unina.it
|
|
C. Musella
Dipartimento di Matematica e Applicazioni
Università di Napoli Federico II
Complesso Universitario Monte S. Angelo
Via Cintia
I–80126 Napoli
Italy
cmusella@unina.it
|
|
|
|
|
Y. P. Sysak
Institute of Mathematics
Ukrainian National Academy of Sciences
vul. Tereshchenkivska 3
01601 Kiev
Ukraine
sysak@imath.kiev.ua
|
|
|
Abstract
|
A subgroup
 of a group of a group
 is said to be permutable if is said to be permutable if
 for each subgroup for each subgroup
 of of  , and the group , and the group
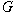 is called quasihamiltonian if all its
subgroups are permutable. We shall say that is called quasihamiltonian if all its
subgroups are permutable. We shall say that
 is a is a  -group if every subgroup -group if every subgroup
 of of
 contains a subgroup contains a subgroup
 of finite index which is permutable in of finite index which is permutable in
 . It is proved that every locally finite . It is proved that every locally finite
 -group contains a quasihamiltonian subgroup of
finite index. In the proof of this result we use
a theorem by Buckley, Lennox, Neumann, Smith and
Wiegold concerning the corresponding problem when
permutable subgroups are replaced by normal
subgroups: if -group contains a quasihamiltonian subgroup of
finite index. In the proof of this result we use
a theorem by Buckley, Lennox, Neumann, Smith and
Wiegold concerning the corresponding problem when
permutable subgroups are replaced by normal
subgroups: if
 is a locally finite group such that is a locally finite group such that
 is finite for every subgroup is finite for every subgroup
 , then , then
 contains an abelian subgroup of finite index. contains an abelian subgroup of finite index.
|
Download the article in PDF format (size 95 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|