J. Aust. Math. Soc.
81 (2006), 165-184
|
Mappings on matrices: invariance of functional values of matrix products
|
Jor-Ting Chan
Department of Mathematics
The University of Hong Kong
Pokfulam Road
Hong Kong
jtchan@hku.hk
|
|
Chi-Kwong Li
Department of Mathematics
College of William and Mary
Williamsburg, VA 23187--8795
USA
ckli@math.wm.edu
|
|
|
Nung-Sing Sze
Department of Mathematics
The University of Hong Kong
Pokfulam Road
Hong Kong
and
Department of Mathematics
University of Connecticut
Storrs, CT 06269-3009
USA
sze@math.uconn.edu
|
|
|
Abstract
|
Let
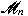 be the algebra of all
be the algebra of all 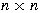 matrices over a field matrices over a field
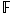 , where , where
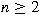 . Let . Let
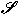 be a subset of
be a subset of
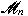 containing all rank one matrices. We study
mappings containing all rank one matrices. We study
mappings 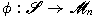 such that
such that
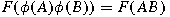 for various families of functions
for various families of functions
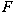 including all the unitary similarity invariant
functions on real or complex matrices. Very
often, these mappings have the form including all the unitary similarity invariant
functions on real or complex matrices. Very
often, these mappings have the form
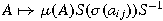 for all
for all 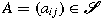 for some invertible
for some invertible 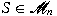 , field monomorphism , field monomorphism
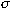 of of
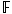 , and an , and an
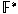 -valued mapping -valued mapping
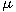 defined on
defined on
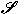 . For real matrices, . For real matrices,
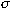 is often the identity map; for complex matrices,
is often the identity map; for complex matrices,
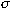 is often the identity map or the conjugation
map: is often the identity map or the conjugation
map:
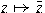 . A key idea in our study is reducing the problem
to the special case when . A key idea in our study is reducing the problem
to the special case when
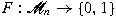 is defined by
is defined by
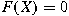 , if , if
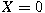 , and , and
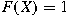 otherwise. In such a case, one needs to
characterize otherwise. In such a case, one needs to
characterize
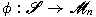 such that
such that
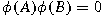 if and only if
if and only if
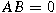 . We show that such a map has the standard form
described above on rank one matrices in . We show that such a map has the standard form
described above on rank one matrices in
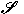 . .
|
Download the article in PDF format (size 163 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|