J. Aust. Math. Soc.  81 (2006), 253-278
Homomorphisms of the algebra of locally integrable functions on the half line

Sandy Grabiner
  Department of Mathematics
  Pomona College
  610 North College Avenue
  Claremont, CA 91711
  USA
  sgrabiner@pomona.edu


Abstract
Let $\phi$ be a continuous nonzero homomorphism of the convolution algebra $L^{1}_{{\rm loc}}(\mathbb{R}^{+})$ and also the unique extension of this homomorphism to $M_{{\rm loc}}(\mathbb{R}^{+})$. We show that the map $\phi$ is continuous in the weak* and strong operator topologies on $M_{{\rm loc}}$, considered as the dual space of $C_{c}(\mathbb{R}^{+})$ and as the multiplier algebra of $L^{1}_{{\rm loc}}$. Analogous results are proved for homomorphisms from $L^{1}[0,a)$ to $L^{1}[0,b)$. 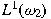For each convolution algebra $L^{1}(\omega_{1})$, $\phi$ restricts to a continuous homomorphism from some $L^{1}(\omega_{1})$ to some $L^{1}(\omega_{2})$, and, for each sufficiently large $L^{1}(\omega_{2})$, $\phi$ restricts to a continuous homomorphism from some $L^{1}(\omega_{1})$ to $L^{1}(\omega_{2})$. We also determine which continuous homomorphisms between weighted convolution algebras extend to homomorphisms of $L^{1}_{{\rm loc}}$. We also prove results on convergent nets, continuous semigroups, and bounded sets in $M_{{\rm loc}}$ that we need in our study of homomorphisms.
Download the article in PDF format (size 211 Kb)
Australian Mathematical Publishing Association Inc. ©  Australian MS