In several recent papers, a one-sided iterative
process for computing positive definite solutions
of the nonlinear matrix equation
 , where , where
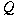 is positive definite, has been studied. In this
paper, a two-sided iterative process for the same
equation is investigated. The novel idea here is
that the two sequences obtained by starting at
two different values provide (a) an interval in
which the solution is located, that is, is positive definite, has been studied. In this
paper, a two-sided iterative process for the same
equation is investigated. The novel idea here is
that the two sequences obtained by starting at
two different values provide (a) an interval in
which the solution is located, that is,
 for all
for all
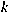 and (b) a better stopping criterion. Some
properties of solutions are discussed. Sufficient
solvability conditions on a matrix and (b) a better stopping criterion. Some
properties of solutions are discussed. Sufficient
solvability conditions on a matrix
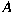 are derived. Moreover, when the matrix
are derived. Moreover, when the matrix
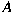 is normal and satisfies an additional condition,
the matrix equation has smallest and largest
positive definite solutions. Finally, some
numerical examples are given to illustrate the
effectiveness of the algorithm. is normal and satisfies an additional condition,
the matrix equation has smallest and largest
positive definite solutions. Finally, some
numerical examples are given to illustrate the
effectiveness of the algorithm.
|