ANZIAM J.
45 (2003), 195-205
|
Degree reduction of Bézier curves using constrained Chebyshev polynomials of the second kind
|
Young Joon Ahn
Department of Mathematics Education
Chosun University
Gwangju 501--759
Korea
ahn@chosun.ac.kr
|
|
|
Abstract
|
In this paper a constrained Chebyshev polynomial
of the second kind with
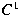 -continuity is proposed as an error function for
degree reduction of Bézier curves with a -continuity is proposed as an error function for
degree reduction of Bézier curves with a
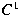 -constraint at both endpoints. A sharp upper
bound of the -constraint at both endpoints. A sharp upper
bound of the
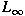 norm for a constrained Chebyshev polynomial of
the second kind with norm for a constrained Chebyshev polynomial of
the second kind with
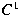 -continuity can be obtained explicitly along with
its coefficients, while those of the constrained
Chebyshev polynomial which provides the best -continuity can be obtained explicitly along with
its coefficients, while those of the constrained
Chebyshev polynomial which provides the best
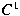 -constrained degree reduction are obtained
numerically. The representations in closed form
for the coefficients and the error bound are very
useful to the users of Computer Graphics or
CAD/CAM systems. Using the error bound in the
closed form, a simple subdivision scheme for -constrained degree reduction are obtained
numerically. The representations in closed form
for the coefficients and the error bound are very
useful to the users of Computer Graphics or
CAD/CAM systems. Using the error bound in the
closed form, a simple subdivision scheme for
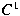 -constrained degree reduction within a given
tolerance is presented. As an illustration, our
method is applied to -constrained degree reduction within a given
tolerance is presented. As an illustration, our
method is applied to
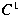 -constrained degree reduction of a plane
Bézier curve, and the numerical result is
compared visually to that of the best degree
reduction method. -constrained degree reduction of a plane
Bézier curve, and the numerical result is
compared visually to that of the best degree
reduction method.
|
Download the article in PDF format (size 150 Kb)
|
|
|
|