J. Austral. Math. Soc.
72 (2002), 223-245
|
On the Toeplitz algebras of right-angled and finite-type Artin groups
|
John Crisp
Laboratoire de Topologie
Université de Bourgogne
UMR 5584 du CNRS
B.P. 47 870
21078 Dijon Cedex
France
crisp@topolog.u-bourgogne.fr
|
|
and
|
Marcelo Laca
Department of Mathematics
The University of Newcastle
NSW 2308 Australia
Current address:
Mathematisches Institut
Westfalische Wilhelms-Universitat
Einsteinstr. 62, 48149 Munster
Germany
laca@math.uni-muenster.de
|
|
|
Abstract
|
between their direct and free products, with the
graph determining which pairs of groups commute.
We show that the graph product of quasi-lattice
ordered groups is quasi-lattice ordered, and,
when the underlying groups are amenable, that it
satisfies Nica's amenability condition for
quasi-lattice orders. The associated Toeplitz
algebras have a universal property, and their
representations are faithful if the generating
isometries satisfy a joint properness condition.
When applied to right-angled Artin groups this
yields a uniqueness theorem for the
C*-algebra generated by a collection of isometries
such that any two of them either
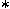 -commute or else have orthogonal ranges. The
analogous result fails to hold for the nonabelian
Artin groups of finite type considered by
Brieskorn and Saito, and Deligne.
|
Download the article in PDF format (size 200 Kb)
|
|
|
|