J. Austral. Math. Soc.
72 (2002), 363-388
|
Vector valued mean-periodic functions on groups
|
P. Devaraj
Department of Mathematics
Indian Institute of Technology
Powai, Mumbai-76
PIN-400076
India
devaraj@math.iitb.ac.in
|
|
and
|
Inder K. Rana
Department of Mathematics
Indian Institute of Technology
Powai, Mumbai-76
PIN-400076
India
ikr@math.iitb.ac.in
|
|
|
Abstract
|
Let  be a locally compact Hausdorff abelian group
and be a locally compact Hausdorff abelian group
and 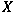 be a complex Banach space. Let be a complex Banach space. Let
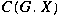 denote the space of all continuous functions denote the space of all continuous functions
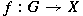 , with the topology of uniform convergence on
compact sets.
Let , with the topology of uniform convergence on
compact sets.
Let 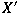 denote the dual of denote the dual of
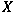 with the weak* topology. Let with the weak* topology. Let
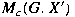 denote the space of all denote the space of all
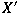 -valued compactly supported regular measures of
finite variation on -valued compactly supported regular measures of
finite variation on
 . For a function . For a function
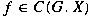 and and
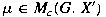 , we define the notion of convolution , we define the notion of convolution
 . A function . A function
 is called mean-periodic if there exists a
non-trivial measure
is called mean-periodic if there exists a
non-trivial measure
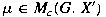 such that
such that
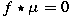 . For . For
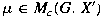 , let , let
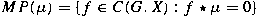 and let
and let
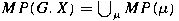 .
In this paper we analyse the following questions: .
In this paper we analyse the following questions:
Is 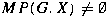 ? ?
Is 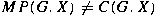 ? ?
Is 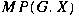 dense in dense in
 ? ?
Is 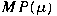 generated by `exponential monomials' in it?
generated by `exponential monomials' in it?
We answer these questions for the groups
 , the real line, and , the real line, and
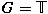 , the circle group. Problems of spectral analysis
and spectral synthesis for , the circle group. Problems of spectral analysis
and spectral synthesis for
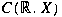 and and
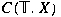 are also analysed. are also analysed.
|
Download the article in PDF format (size 232 Kb)
|
|
|
|