J. Aust. Math. Soc.
74 (2003), 165-171
|
Betti numbers of fixed point sets and multiplicities of indecomposable summands
|
|
|
Abstract
|
Let
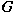 be a finite group of even order, be a finite group of even order,
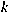 be a field of characteristic 2, and be a field of characteristic 2, and
 be a finitely generated be a finitely generated
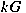 -module. If -module. If
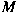 is realized by a compact is realized by a compact
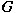 -Moore space -Moore space
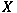 , then the Betti numbers of the fixed point set , then the Betti numbers of the fixed point set
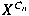 and the multiplicities of indecomposable
summands of and the multiplicities of indecomposable
summands of
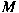 considered as a considered as a
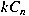 -module are related via a localization theorem in
equivariant cohomology, where -module are related via a localization theorem in
equivariant cohomology, where
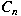 is a cyclic subgroup of is a cyclic subgroup of
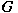 of order of order 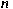 . Explicit formulas are given for . Explicit formulas are given for
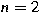 and and 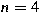 . .
|
Download the article in PDF format (size 64 Kb)
|
|
|
|