J. Aust. Math. Soc.  74 (2003), 331-350
Embeddings of $\ell_p$ into non-commutative spaces

Narcisse Randrianantoanina
  Department of Mathematics and Statistics
  Miami University
  Oxford, Ohio 45056
  USA
  randrin@muohio.edu


Abstract
Let 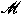$\mathcal{M}$ be a semi-finite von Neumann algebra equipped with a faithful normal trace $\tau$. We prove a Kadec-Pelczynski type dichotomy principle for subspaces of symmetric space of measurable operators of Rademacher type 2. We study subspace structures of non-commutative Lorentz spaces $L_{p,q}(\mathcal{M}, \tau)$, extending some results of Carothers and Dilworth to the non-commutative settings. In particular, we show that, under natural conditions on indices, $\ell_p$ cannot be embedded into $L_{p,q}(\mathcal{M}, \tau)$. 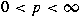As applications, we prove that for $0<p<\infty$ with $p \neq 2$, $\ell_p$ cannot be strongly embedded into $L_p(\mathcal{M},\tau)$. This provides a non-commutative extension of a result of Kalton for $0<p<1$ and a result of Rosenthal for $1\leq p <2$ on $L_p[0,1]$.
Download the article in PDF format (size 177 Kb)
TeXAdel Scientific Publishing ©  Australian MS