J. Aust. Math. Soc.
75 (2003), 23-40
|
On products in lattice-ordered algebras
|
Karim Boulabiar
Département des Classes Préparatoires
Institut Préparatoire aux Etudes Scientifiques et Techniques
Université 7 Novembre à Carthage
BP 51, 2070-La Marsa
Tunisia
karim.boulabiar@ipest.rnu.tn
|
|
|
Abstract
|
Let
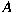 be a uniformly complete vector sublattice of an
Archimedean semiprime be a uniformly complete vector sublattice of an
Archimedean semiprime
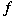 -algebra -algebra
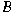 and and 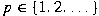 . It is shown that the set . It is shown that the set
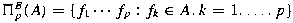 is a uniformly complete vector sublattice of
is a uniformly complete vector sublattice of
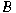 . Moreover, if . Moreover, if
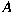 is provided with an almost is provided with an almost
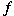 -algebra multiplication -algebra multiplication
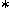 then there exists a positive operator then there exists a positive operator
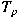 from from
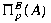 into into
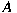 such that such that 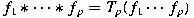 for all
for all
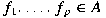 . As application, being given a uniformly
complete almost . As application, being given a uniformly
complete almost
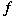 -algebra -algebra
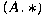 and a natural number and a natural number
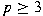 , the set , the set
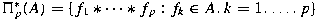 is a uniformly complete semiprime
is a uniformly complete semiprime
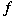 -algebra under the ordering and the
multiplication inherited from -algebra under the ordering and the
multiplication inherited from
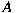 . .
|
Download the article in PDF format (size 139 Kb)
|
|
|
|