J. Aust. Math. Soc.
75 (2003), 413-422
|
On  -direct sums of Banach spaces and convexity -direct sums of Banach spaces and convexity
|
|
|
|
|
Takayuki Tamura
Graduate School of Social Sciences and Humanities
Chiba University
Chiba 263-8522
Japan
tamura@le.chiba-u.ac.jp
|
|
|
Abstract
|
Let  be Banach spaces and be Banach spaces and
 a continuous convex function with some
appropriate conditions on a certain convex set in a continuous convex function with some
appropriate conditions on a certain convex set in
 . Let . Let
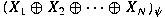 be the direct sum of
be the direct sum of  equipped with the norm associated with equipped with the norm associated with
 . We characterize the strict, uniform, and
locally uniform convexity of . We characterize the strict, uniform, and
locally uniform convexity of
 by means of the convex function
by means of the convex function
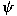 . As an application these convexities are
characterized for the . As an application these convexities are
characterized for the
 -sum -sum
 (
( , ,
 ), which includes the well-known facts for the ), which includes the well-known facts for the
 -sum -sum
 in the case
in the case  . .
|
Download the article in PDF format (size 91 Kb)
|
|
|
|