J. Aust. Math. Soc.
76 (2004), 151-165
|
An application of Moser iteration to complete minimal submanifolds in a sphere
|
Leung-Fu Cheung
Department of Applied Mathematics
The Hong Kong Polytechnic University
Hung Hom Kowloon
Hongkong
malfcheu@hkpu07.polyu.edu.hk
|
|
|
Pui-Fai Leung
Department of Mathematics
National University of Singapore
Lower Kent Ridge Road
Singapore 119260
Singapore
matfredl@nus.edu.sg
|
|
|
Abstract
|
We apply the Moser iteration method to obtain a
pointwise bound on the norm of the second
fundamental form from a bound on
its 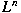 norm for a complete minimal submanifold in a
sphere. As an application we show that a complete
minimal submanifold in a sphere with finite total
curvature and Ricci curvature bounded away
from norm for a complete minimal submanifold in a
sphere. As an application we show that a complete
minimal submanifold in a sphere with finite total
curvature and Ricci curvature bounded away
from 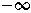 must be compact. This complements similar
results of Osserman and Oliveira in the case the
ambient space is the Euclidean and the hyperbolic
space respectively. must be compact. This complements similar
results of Osserman and Oliveira in the case the
ambient space is the Euclidean and the hyperbolic
space respectively.
|
Download the article in PDF format (size 112 Kb)
|
|
|
|