J. Aust. Math. Soc.
76 (2004), 189-206
|
Composition operators in Orlicz spaces
|
Yunan Cui
Department of Mathematics
Harbin University of Sciences and Technology
52 Xuefu Road, Nanang. Dist.
Harbin, Heilongjiang 150080 P. R. of China
cuiya@mail.hrbust.edu.cn
|
|
Henryk Hudzik
Faculty of Mathematics
and Computer Science
Adam Mickiewicz University
Umultowska 87
61-614 Poznan
Poland
hudzik@amu.edu.pl
|
|
|
|
|
|
Lech Maligranda
Department of Mathematics
Lulea University of Technology
SE-97187 Lulea
Sweden
lech@sm.luth.se
|
|
|
Abstract
|
Composition operators 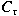 between Orlicz
spaces between Orlicz
spaces 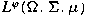 generated
by measurable and nonsingular
transformations generated
by measurable and nonsingular
transformations 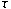 from from 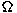 into itself are considered. We characterize
boundedness and compactness of the composition
operator between Orlicz spaces in terms of
properties of
the mapping into itself are considered. We characterize
boundedness and compactness of the composition
operator between Orlicz spaces in terms of
properties of
the mapping 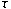 , the function , the function 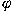 and the measure space and the measure space  . These
results generalize earlier results known
for . These
results generalize earlier results known
for 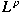 -spaces. -spaces.
|
Download the article in PDF format (size 147 Kb)
|
|
|
|