J. Aust. Math. Soc.
76 (2004), 269-280
|
Nuclear and integral polynomials
|
Raffaella Cilia
Dipartimento di Matematica
Facoltà di Scienze
Università di Catania
Viale Andrea Doria 6
95100 Catania
Italy
cilia@dmi.unict.it
|
|
|
Joaquín M. Gutiérrez
Departamento de Matemática Aplicada
ETS de Ingenieros Industriales
Universidad Politécnica de Madrid
C. José Gutiérrez Abascal 2
28006 Madrid
Spain
jgutierrez@etsii.upm.es
|
|
|
Abstract
|
Let
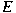 be a Banach space whose dual be a Banach space whose dual
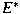 has the approximation property, and let has the approximation property, and let
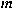 be an index. We show that be an index. We show that
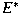 has the Radon-Nikodým property if and
only if every has the Radon-Nikodým property if and
only if every 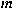 -homogeneous integral polynomial from -homogeneous integral polynomial from
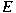 into any Banach space is nuclear. We also obtain
factorization and composition results for nuclear
polynomials. into any Banach space is nuclear. We also obtain
factorization and composition results for nuclear
polynomials.
|
Download the article in PDF format (size 107 Kb)
|
|
|
|