J. Aust. Math. Soc.
76 (2004), 291-302
|
Generalized Weyl's theorem and hyponormal operators
|
M. Berkani
Groupe d'Analyse et Théorie des Opérateurs (G.A.T.O.)
Université Mohammed I
Faculté des Sciences
Département de Mathématiques
Oujda
Morocco
berkani@sciences.univ-oujda.ac.ma
|
|
|
A. Arroud
Groupe d'Analyse et Théorie des Opérateurs (G.A.T.O.)
Université Mohammed I
Faculté des Sciences
Département de Mathématiques
Oujda
Morocco
arroud@sciences.univ-oujda.ac.ma
|
|
|
Abstract
|
Let 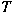 be a bounded linear operator acting on a Hilbert
space be a bounded linear operator acting on a Hilbert
space 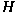 . The . The
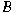 -Weyl spectrum of -Weyl spectrum of
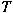 is the set is the set
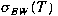 of all of all
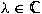 such that
such that 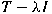 is not a is not a
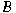 -Fredholm operator of index 0. Let -Fredholm operator of index 0. Let
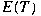 be the set of all isolated eigenvalues of be the set of all isolated eigenvalues of
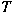 . The aim of this paper is to show that if . The aim of this paper is to show that if
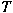 is a hyponormal operator, then is a hyponormal operator, then
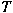 satisfies generalized Weyl's theorem satisfies generalized Weyl's theorem
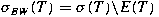 , and the , and the
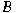 -Weyl spectrum -Weyl spectrum
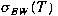 of of
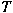 satisfies the spectral mapping theorem. We also
consider commuting finite rank perturbations of
operators satisfying generalized Weyl's theorem. satisfies the spectral mapping theorem. We also
consider commuting finite rank perturbations of
operators satisfying generalized Weyl's theorem.
|
Download the article in PDF format (size 100 Kb)
|
|
|
|