J. Aust. Math. Soc.
76 (2004), 207-221
|
Boundedness of vector-valued martingale transforms on extreme points and applications
|
Teresa Martínez
Departamento de Matemáticas
Universidad Autónoma de Madrid
Ciudad Universitaria de Canto Blanco
28049 Madrid
Spain
teresa.martinez@uam.es
|
|
|
José L. Torrea
Departamento de Matemáticas
Universidad Autónoma de Madrid
Ciudad Universitaria de Canto Blanco
28049 Madrid
Spain
joseluis.torrea@uam.es
|
|
|
Abstract
|
Let 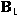 , , 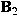 be a pair of Banach spaces and be a pair of Banach spaces and
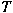 be a vector valued martingale transform (with
respect to general filtration) which
maps be a vector valued martingale transform (with
respect to general filtration) which
maps 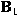 -valued martingales into -valued martingales into
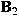 -valued martingales. Then, the following
statements are equivalent: -valued martingales. Then, the following
statements are equivalent:
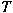 is bounded
from is bounded
from 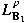 into into 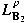 for some for some
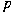 (or equivalently for every (or equivalently for every
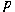 ) in the range ) in the range
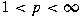 ; ;
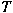 is bounded from is bounded from
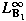 into
into
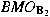 ; ;
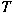 is bounded from is bounded from
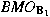 into into
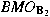 ; ;
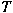 is bounded from is bounded from
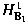 into into
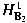 . Applications to . Applications to
 and martingale cotype properties are given. We
also prove that the Hardy space and martingale cotype properties are given. We
also prove that the Hardy space
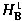 defined in the case of a general filtration has
nice dense sets and nice atomic decompositions if
and only if
defined in the case of a general filtration has
nice dense sets and nice atomic decompositions if
and only if
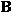 has the Radon-Nikodým property. has the Radon-Nikodým property.
|
Download the article in PDF format (size 141 Kb)
|
|
|
|