J. Aust. Math. Soc.
76 (2004), 425-447
|
One-sided ideals and approximate identities in operator algebras
|
David P. Blecher
Department of Mathematics
University of Houston
4800 Calhoun
Houston, TX 77204-3008
USA
dblecher@math.uh.edu
|
|
|
Abstract
|
A left ideal of any
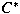 -algebra is an example of an operator algebra
with a right contractive approximate identity
(r.c.a.i.). Indeed, left ideals in -algebra is an example of an operator algebra
with a right contractive approximate identity
(r.c.a.i.). Indeed, left ideals in
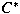 -algebras may be characterized as the class of
such operator algebras, which happen also to be
triple systems. Conversely, we show here and in a
sequel to this paper, that operator algebras with
r.c.a.i. should be studied in terms of a certain
left ideal of a -algebras may be characterized as the class of
such operator algebras, which happen also to be
triple systems. Conversely, we show here and in a
sequel to this paper, that operator algebras with
r.c.a.i. should be studied in terms of a certain
left ideal of a 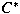 -algebra. We study left ideals from the
perspective of `Hamana theory' and using the
multiplier algebras of an operator space studied
elsewhere by the author. More generally, we
develop some general theory for operator algebras
which have a 1-sided identity or approximate
identity, including a Banach-Stone theorem for
these algebras, and an analysis of the
`multiplier operator algebra'. -algebra. We study left ideals from the
perspective of `Hamana theory' and using the
multiplier algebras of an operator space studied
elsewhere by the author. More generally, we
develop some general theory for operator algebras
which have a 1-sided identity or approximate
identity, including a Banach-Stone theorem for
these algebras, and an analysis of the
`multiplier operator algebra'.
|
Download the article in PDF format (size 190 Kb)
|
|
|
|