J. Aust. Math. Soc.
77 (2004), 1-16
|
Isometries between matrix algebras
|
Wai-Shun Cheung
Center of Linear Algebra and Combinatorics
University of Lisbon
Lisbon
Portugal
Current address:
Department of Mathematics
University of Hong Kong
Hong Kong
a9000068@yahoo.com
|
|
Chi-Kwong Li
Department of Mathematics
College of William and Mary
P.O. Box 8795
Williamsburg
Virginia 23187-8795
USA
ckli@math.wm.edu
|
|
|
Yiu-Tung Poon
Department of Mathematics
Iowa State University
Ames
Iowa 50011
USA
ytpoon@iastate.edu
|
|
|
Abstract
|
As an attempt to understand linear isometries
between 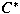 -algebras without the surjectivity assumption, we
study linear isometries between matrix algebras.
Denote by -algebras without the surjectivity assumption, we
study linear isometries between matrix algebras.
Denote by 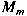 the algebra of the algebra of
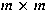 complex matrices.
If complex matrices.
If 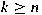 and and 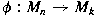 has the form has the form
![$X \mapsto U[X \oplus f(X)]V$](img_files_abstracts/l28-img5.png) or or ![$X \mapsto U[X^t \oplus f(X)]V$](img_files_abstracts/l28-img6.png) for some unitary
for some unitary 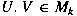 and contractive linear map and contractive linear map
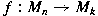 , then , then
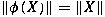 for all for all
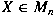 . We prove that the converse is true if . We prove that the converse is true if
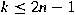 , and the converse may fail if , and the converse may fail if
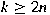 . Related results and questions involving
positive linear maps and the numerical range are
discussed. . Related results and questions involving
positive linear maps and the numerical range are
discussed.
|
Download the article in PDF format (size 127 Kb)
|
|
|
|