J. Aust. Math. Soc.
77 (2004), 91-110
|
Ideals of compact operators
|
Asvald Lima
Department of Mathematics
Agder College
Gimlemoen 25J
Serviceboks 422
4604 Kristiansand
Norway
asvald.lima@hia.no
|
|
|
Eve Oja
Faculty of Mathematics
Tartu University
Liivi 2-606
EE-50409 Tartu
Estonia
eveoja@math.ut.ee
|
|
|
Abstract
|
We give an example of a Banach space
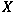 such that such that
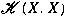 is not an ideal in is not an ideal in
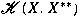 . We prove that if . We prove that if
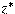 is a weak is a weak
 denting point in the unit ball of denting point in the unit ball of
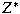 and if and if
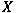 is a closed subspace of a Banach space is a closed subspace of a Banach space
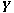 , then the set of norm-preserving extensions , then the set of norm-preserving extensions
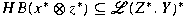 of a functional
of a functional 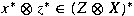 is equal to the set is equal to the set
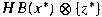 . Using this result, we show that if . Using this result, we show that if
 is an is an
 -ideal in -ideal in
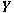 and and 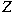 is a reflexive Banach space, then is a reflexive Banach space, then
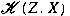 is an is an
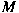 -ideal in -ideal in
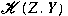 whenever whenever
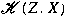 is an ideal in is an ideal in
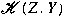 . We also show that . We also show that
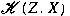 is an ideal (respectively, an
is an ideal (respectively, an
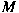 -ideal) in -ideal) in
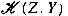 for all Banach spaces for all Banach spaces
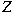 whenever whenever 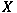 is an ideal (respectively, an is an ideal (respectively, an
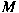 -ideal) in -ideal) in
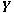 and and
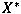 has the compact approximation property with
conjugate operators. has the compact approximation property with
conjugate operators.
|
Download the article in PDF format (size 171 Kb)
|
|
|
|