J. Aust. Math. Soc.
77 (2004), 371-385
|
An
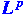 version of Hardy's theorem for the Dunkl transform version of Hardy's theorem for the Dunkl transform
|
Léonard Gallardo
Faculté des Sciences
Département de Mathématiques
Parc de Grandmont
37200 Tours
France
gallardo@univ-tours.fr
|
|
|
Khalifa Trimèche
Faculté des Sciences de Tunis
Département de Mathématiques
Campus Universitaire
1060 Tunis
Tunisie
khlifa.trimeche@fst.rnu.tn
|
|
|
Abstract
|
In this paper, we give a generalization of Hardy's theorems for the Dunkl
transform 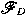 on on 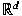 . More precisely for all . More precisely for all
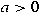 , , 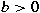 and and ![$p, q \in [1, + \infty]$](img_files_abstracts/q116-img4.png) , we determine the measurable functions , we determine the measurable functions
 on on 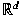 such that
such that 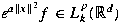 and
and 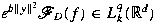 , where , where
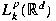 are the Lebesgue spaces associated with the
Dunkl transform. are the Lebesgue spaces associated with the
Dunkl transform.
|
Download the article in PDF format (size 133 Kb)
|
|
|
|