J. Aust. Math. Soc.
78 (2005), 149-166
|
Explicit formulae for two-bridge knot polynomials
|
Shinji Fukuhara
Department of Mathematics
Tsuda College
Tsuda-machi 2-1-1
Kodaira-shi
Tokyo 187-8577
Japan
fukuhara@tsuda.ac.jp
|
|
|
Abstract
|
A two-bridge knot (or link) can be characterized
by the so-called Schubert normal form 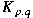 where where 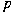 and and 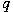 are positive coprime integers. Associated to are positive coprime integers. Associated to 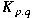 there are the Conway polynomial there are the Conway polynomial 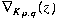 and the normalized Alexander
polynomial and the normalized Alexander
polynomial 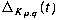 . However, it has been open problem how . However, it has been open problem how
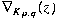 and and 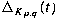 are expressed in terms
of are expressed in terms
of 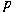 and and 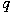 . In this note, we will give explicit formulae
for the Conway polynomials and the normalized
Alexander polynomials in the case of two-bridge
knots and links. This is done using elementary
number theoretical functions in . In this note, we will give explicit formulae
for the Conway polynomials and the normalized
Alexander polynomials in the case of two-bridge
knots and links. This is done using elementary
number theoretical functions in 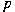 and and 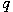 . .
|
Download the article in PDF format (size 124 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|