J. Aust. Math. Soc.
78 (2005), 199-210
|
Boundedness of sign-preserving charges, regularity, and the completeness of inner product spaces
|
Emmanuel Chetcuti
Mathematical Institute
Slovak Academy of Sciences
Stefánikova 49
SK-814 73 Bratislava
Slovakia
chetcuti@mat.savba.sk
|
|
|
Anatolij Dvurecenskij
Mathematical Institute
Slovak Academy of Sciences
Stefánikova 49
SK-814 73 Bratislava
Slovakia
dvurecen@mat.savba.sk
|
|
|
Abstract
|
We introduce sign-preserving charges on the
system of all orthogonally closed subspaces,
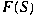 , of an inner product space , of an inner product space
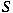 , and we show that it is always bounded on all
the finite-dimensional subspaces whenever , and we show that it is always bounded on all
the finite-dimensional subspaces whenever
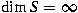 . When . When
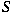 is finite-dimensional this is not true. This
fact is used for a new completeness criterion
showing that is finite-dimensional this is not true. This
fact is used for a new completeness criterion
showing that 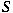 is complete whenever is complete whenever
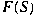 admits at least one non-zero sign-preserving
regular charge. In particular, every such charge
is always completely additive. admits at least one non-zero sign-preserving
regular charge. In particular, every such charge
is always completely additive.
|
Download the article in PDF format (size 103 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|