J. Aust. Math. Soc.
78 (2005), 257-272
|
Iterative methods for computing generalized inverses related with optimization methods
|
Dragan S. Djordjevic
Department of Mathematics
University of Nis
Faculty of Science and Mathematics
P.O. Box 224
Visegradska 33
18000 Nis
Serbia
dragan@pmf.ni.ac.yu
|
|
|
Predrag S. Stanimirovic
Department of Mathematics
University of Nis
Faculty of Science and Mathematics
P.O. Box 224
Visegradska 33
18000 Nis
Serbia
pecko@pmf.ni.ac.yu
|
|
|
Abstract
|
We develop several iterative methods for
computing generalized inverses using both first
and second order optimization methods in 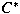 -algebras. Known steepest descent iterative
methods are generalized in -algebras. Known steepest descent iterative
methods are generalized in
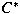 -algebras. We introduce second order methods
based on the minimization of the norms -algebras. We introduce second order methods
based on the minimization of the norms
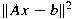 and and 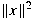 by means of the known second order
unconstrained minimization methods. We give
several examples which illustrate our theory. by means of the known second order
unconstrained minimization methods. We give
several examples which illustrate our theory.
|
Download the article in PDF format (size 129 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|