J. Aust. Math. Soc.
78 (2005), 291-295
|
Elements of prime power order and their conjugacy classes in finite groups
|
László Héthelyi
Department of Algebra
Technical University of Budapest
H-1521 Budapest
Hungary
hethelyi@math.bme.hu
|
|
|
|
|
Abstract
|
We show that, for any positive integer 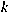 , there are only finitely many finite groups, up
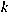to isomorphism, with exactly  conjugacy classes of elements of prime power
order. This generalizes a result of E. Landau
from 1903. The proof of our generalization makes
use of the classification of finite simple
groups.
|
Download the article in PDF format (size 41 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|