J. Aust. Math. Soc.
78 (2005), 323-338
|
Weyl quantization and a symbol calculus for abelian groups
|
|
|
Abstract
|
We develop a notion of a 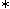 -product on a general abelian group, establish a
Weyl calculus for operators on the group and
connect these with the representation theory of
an associated Heisenberg group. This can all be
viewed as a generalization of the familiar theory
for -product on a general abelian group, establish a
Weyl calculus for operators on the group and
connect these with the representation theory of
an associated Heisenberg group. This can all be
viewed as a generalization of the familiar theory
for 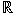 . A symplectic group is introduced and a
connection with the classical Cayley transform is
established. Our main application is to finite
groups, where consideration of the symbol
calculus for the cyclic groups provides an
interesting alternative to the usual matrix form
for linear transformations. This leads to a new
basis for . A symplectic group is introduced and a
connection with the classical Cayley transform is
established. Our main application is to finite
groups, where consideration of the symbol
calculus for the cyclic groups provides an
interesting alternative to the usual matrix form
for linear transformations. This leads to a new
basis for 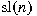 and a decomposition of this Lie algebra into a
sum of Cartan subalgebras. and a decomposition of this Lie algebra into a
sum of Cartan subalgebras.
|
Download the article in PDF format (size 119 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|