J. Aust. Math. Soc.  79 (2005), 113-130
Finite-dimensional odd Hamiltonian superalgebras over a field of prime characteristic

Wende Liu
  Department of Mathematics
  Harbin Normal University
  Harbin 150080
  China
  and
  Department of Mathematics
  Northeast Normal University
  Changchun 130024
  China
  wendeliu@sohu.com
and
Yongzheng Zhang
  Department of Mathematics
  Harbin Normal University
  Harbin 150080
  China
  zhyz@nenu.edu.cn


Abstract
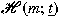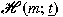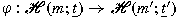Let $\mathcal{H} (m;\underline{t})$ be the finite-dimensional odd Hamiltonian superalgebra over a field of prime characteristic. 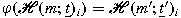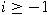By determining ad-nilpotent elements in the even part, the natural filtration of $ \mathcal{H} (m;\underline{t})$ is proved to be invariant in the following sense: If $\varphi: \mathcal{H} (m;\underline{t})\to \mathcal{H} (m';\underline{t}')$ is an isomorphism then $\varphi(\mathcal{H} (m;\underline{t})_i)= \mathcal{H} (m';\underline{t}')_i$ for all $i\geq-1$. Using the result, we complete the classification of odd Hamiltonian superalgebras. Finally, we determine the automorphism group of the restricted odd Hamiltonian superalgebra and give further properties.
Download the article in PDF format (size 171 Kb)
Australian Mathematical Publishing Association Inc. ©  Australian MS