J. Aust. Math. Soc.  80 (2006), 105-130
The turnpike result for approximate solutions of nonautonomous variational problems

Alexander J. Zaslavski
  Department of Mathematics
  Technion-Israel Institute of Technology
  32000, Haifa
  Israel
  ajzasl@techunix.technion.ac.il


Abstract
In this work we study the structure of approximate solutions of variational problems with continuous integrands 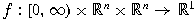$f:[0,\infty) \times \mathbb{R}^n\times \mathbb{R}^n \to \mathbb{R}^1$ which belong to a complete metric space of functions. The main result in this paper deals with the turnpike property of variational problems. To have this property means that the approximate solutions of the problems are determined mainly by the integrand, and are essentially independent of the choice of interval and endpoint conditions, except in regions close to the endpoints.
Download the article in PDF format (size 218 Kb)
Australian Mathematical Publishing Association Inc. ©  Australian MS